Word 2010での行形式による数式の挿入（簡略版）

Word 2010での数式ツールの起動

数式を入力したい位置にカーソルを置いて、次のいずれかの操作により数式ツールを起動します

• 「挿入」タブをクリックし、右端の[π数式]をクリックする。　（数式エディターの起動）
  左端の[標準テキスト]を２度クリックする。　（斜体にする）
• ShiftキーとAlt キーと = キーを同時に押す。　（数式エディターの起動）
  Ctrl キーと i キーを同時に押す。　（斜体にする）

※　Windows版のWordでは、数式部分の文字が自動的に数学文字になりません。そのため、利用者がフォントのスタイルを斜体に変更する必要があります。（PowerPointやMac版のWordでは、自動的に数学文字になります。）

「数式の挿入」の終了

• 「数式の挿入」ボックスの外をクリックする。
• Enterキーを押す。

※　Enterキーを押して不都合が生じる場合は、→（右カーソルキー）でブロックを抜けてから、Enterキーを押してください。

Word 2010での行形式による数式の入力方法

• 行形式による数式入力の記法やASCII文字からの変換を有効にするには、入力後にスペースを入力します。
• + - = & @ などを入力すると、（スペースを入力しなくても）その前の部分は自動的に解釈されます。
• 自動的に解釈してほしくない場合は、（　）でくくります。

以下の説明で、■はスペースの入力、■は→（カーソルキー）でブロックを抜ける操作を示します。

\ は、日本語キーボードでは、￥になります。

文字・記号

• ギリシャ文字や特殊な記号は、ASCII文字列から変換することができます。
• ASCII文字変換では入力できない文字や記号は、数式ツールの「デザイン」タブから選択するか、記号と特殊文字の挿入を利用してください。かな漢字変換による入力を利用することもできます。

分数

• /　の前後の連続する文字はすべて分母・分子になります。
• 連続しない文字を分数にする場合は、( ) でくくります。

Wordでの入力	表　示
ab/2■
(a+b)/2■

上付き・下付き

• ^　の後に続く文字が上付きになります。
• _　の後に続く文字が下付きになります。
• 連続する文字はすべて上付き・下付きになります。
• 連続しない文字を上付き・下付きにする場合は、( ) でくくります。

Wordでの入力	表　示
x^2■
z_ij■

区切り文字

• かっこは中身の大きさに応じてサイズ調整されます。
• 片側だけのかっこを表示するために、特殊な区切り文字が用意されています。開き側は\openもしくは\left、閉じ側は\closeまたは\rightから変換できます。

Wordでの入力	表　示
(x+y)^2■
{\eqarray(x@y@z)}■
{\eqarray(5x+3y=11@12x-4y=4)■\close■■

演算子

• +  -  /  >  <  :  !  = 　以外は、ASCII文字変換を利用して入力します。

Wordでの入力	表　示
a\div■b
a\times■b

累和・累積記号/微分・積分

• 累和・累積記号などは、n項演算子を表す文字列の後に、_ や ^ を付けて上付き・下付き文字を書いてからスペースキーを押します。

Wordでの入力	表　示
\sum_(i=1)^n■i^2■■
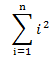\int■_-\infty^\infty■■e^(-x^2■）■dx■

関数

• よく使われる関数の場合は、関数名の後にスペースを入力すると、斜体ではなく正体になります。

Wordでの入力	表　示
sin^2■x

平方根

• √の後ろの連続する文字はすべて平方根の中に入ります。

Wordでの入力	表　示
\sqrt■ｘ■>\cbrt■ｘ■